今回はアニマソラリス10周年ということで、久しぶりにコラムを復活させてみました。
ちょっと行き当りばったりな企画なので、うまくいくとよいのですが。 なんでこんな内容をテーマに選んだかというと、特殊相対性理論ででてくるミンコフスキー空間で、時間軸が虚数的になっていることから、関連があるかな、と思ったからなんですね。
まぁ、結論から言ってしまうと、複素平面はそのままではミンコフスキー空間にはならなかったりします。 まぁ、タイトルにある複素平面といきなり出されても、意味のわからない人の方が大勢でしょう。そこで、まずは順を追って簡単な方から話を進めていくことにしましょう。
まずは自然数から。自然数といっても、難しく考える必要はありません。要は小学校の算数で習う数のことです。1,2,3,……といった数字のことですね。これはおもしろい特徴があって、自然数同士の足し算は必ず自然数になります。あたりまえと言うなかれ。数学というのは、こういったあたりまえのことを積み重ねていくことでできあがっていくのです。
さて。この自然数をグラフに表してみましょう。 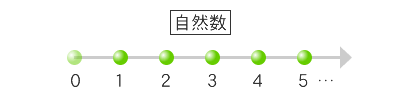
0は自然数に含めるときと含めないときがありますが、それはどういう定義をしているかで違うだけで、とりあえずはどちらでも良いです。ここでは厳密は定義はしていないので、便宜的に0は含めておきましょう。図を見ていただけるとわかると思いますが、0から右の方に等間隔に数字が並んでいます。
足し算は、例えば2たす3などの場合は2の位置から3つ位置を右にずらすことで結果が得られます。
小学校では、他にも重要な演算を習いますね。そう。引き算です。引き算もこの自然数のグラフから計算することができます。足し算のときは右に位置をずらしていましたが、引き算のときは左に位置をずらしていけばよいのです。これで小学校の低学年までの引き算の計算は簡単にできることがわかるでしょう。例えば3ひく2の場合は、3の位置から2つ位置を左にずらすことで結果が出ます。
さて、小学校の低学年までと断ったのは、意味があります。例えば2ひく3などの計算をしようとすると、自然数のグラフからはみ出してしまいます。引く数の方が大きいときには自然数では足りないのです。
そこで、自然数のグラフを左に広げて、新しい領域を作ってみましょう。 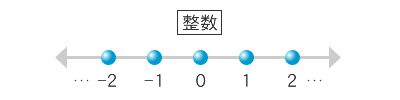
0から左の方に等間隔に-1,-2,-3,……と続いていきます。これを整数といいます。
整数の世界では足し算と引き算をしても、また整数に戻るという性質があるのです。これを、整数は足し算と引き算について閉じているという言い方をします。
小学校で習う演算には他にかけ算と割り算があります。かけ算は足し算をくりかえし行う行為でしかないので、自然数もかけ算について閉じているし、整数についてもかけ算で閉じています。
では、割り算は?
9割る3は3ですから閉じているようにも見えますが……。でも1割る3だったらどうでしょう。ひとつの目盛を3等分するのですから、ひとつの整数の目盛では表現しきれないことがわかります。
ちょっとずるをして、整数のグラフからはなれて電卓をたたいてみると、答えは0.333333……といった数字になります。0.というのは1より小さい数字を表すための表記ですね。まぁ、大抵の人は知っていると思いますけど、この1割る3は3が無限個続く数字になっています。1割る4はどうでしょうか。こちらは0.25でぴったりと決まります。
実はこのように整数のひと目盛の間には割り算で表すことができる数が無限個存在しているのです。これを有理数といいます。4割る1が4であるように、整数そのものも、有理数になっていることがわかります。
さて段々難しくなってきました。
さて、これで私達のグラフが完成に近付いてきたように思えますが、有理数で、このグラフの中に含まれる点を全て表すことができるのでしょうか。
ここで天下り的になってしまいますが、割り算で表現できない数があるということを紹介しましょう。
よく知られているのは、円周率のπです。3.1415……というように無限に続く数なのですが、これは割り算では表すことができない数字となっています。他にもよく使われる数字としては、自然対数の低 e なんかですね。例えば2の平方根(同じ数をかけ合わせたときにその数になる数)は1.414213……と無限に続く数字になっているし、これも割り算では表すことができません。まぁ、そこまで行くとかなり難しくなるので、ここではあまりつっこまないでいて、このような数字が実は有理数の数よりも大量に存在するということを指摘するだけにしておきます。このような割り算で表すことができない数字の全体を無理数と呼んでいます。
そして、有理数と無理数を合わせたものを実数と呼んでいます。実数は、足し算、引き算、かけ算、割り算、そして正の数の平方根の計算について閉じています。
さて、ここで問題です。負の数の平方根は?
実は負の数の平方根は実数では表すことができないのです。
そこで、記号 i というのを用いて、i かける i をマイナス1となる数だとします。すると、負の平方根は実数にこの i をかけた数字で表すことができるのです。まぁ、とりあえず理屈は抜きにして、そういうものだとここでは思ってください。この実数に i をかけた数字のことを純虚数といい、 i のことを虚数単位と呼びます。
さあて、そこで複素数の登場です。複素数はこの純虚数と実数の足し算で表現することができるのです。こんな複雑な複素数がなんで必要かというと、二次方程式の解を全て表現するために必要だったからです。数学では、何かで表現しきれないような場合に、その枠組を拡張していくということをやるんですよ。
さて、これだけだと、なんだかよくわからないままに終わってしまうかと思いますので、複素数をもうちょっとわかりやすい形に表現できないか考えてみましょう。
複素数は上で述べたとおり、実数の部分と、純虚数の部分からなっています。このふたつは足し算引き算ではまじり合わない性質を持っています。足し算引き算は基本的な演算なので、まずはそれから考えてみるわけです。ふたつの数字からできているということから、これを直線だけで表すことはできません。でも、平面にすれば……。 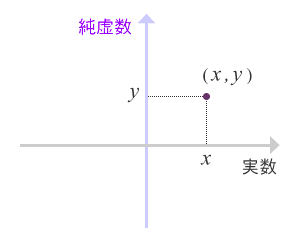
そうして考えだされたのがこの複素平面というやつです。いわゆるx軸の方に実数を取って、y軸の方に純虚数を取るわけです。
ここで、おもしろいことを考えてみます。平面の(1,0)のところにあるのは実数の1なのですが、これに(0,1)、つまり i をかけてやります。複素数のかけ算の方法は実数のときと同じです。1 かける i で i ですね。つまり(0,1)になったわけです。ここで気付いた人がいるかもしれませんが、(1,0)に(0,1)をかけるということは、この複素平面で90度反時計回りに回転させることだということに相当するのです。では、もう一度(0,1)をかけると、90度回転させることになりますから、(-1,0)になることが想像できますね。この(-1,0)というのはそのまんま -1 ですから、結局、 i を2回かけると -1 になるという元の定義に戻ることとなるのです。 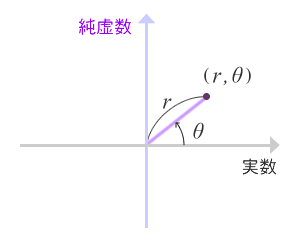
このように、複素数のかけ算は複素平面での回転に関係があるということがなんとなくわかっていただけたでしょうか。
これをもうちょっとわかりやすいようにするために、複素平面のもうひとつの表現方法を考えてみましょう。
極座標というのを御存知でしょうか。原点からの距離と、x軸からの回転角度で平面上の点を表す方法です。すると0からの距離。つまり複素数の大きさと、実数軸からの角度のふたつの数字で複素数をあらわすことができます。この方法で表したとき、複素数のかけ算は、大きさのかけ算と、角度の和であらわすことができるのです。なぜそうなるかは、ちょっと難しい話になってしまい、どうしても数式を使わないで表すことはできないので、ここでは省略します。興味のある方はオイラーの法則で調べてみてください。
さて、こうして角度で表された複素数は、回転とか振動とかを表すのに便利だということがわかっています。振り子の動きを表したりするのに大活躍するわけだったりします。 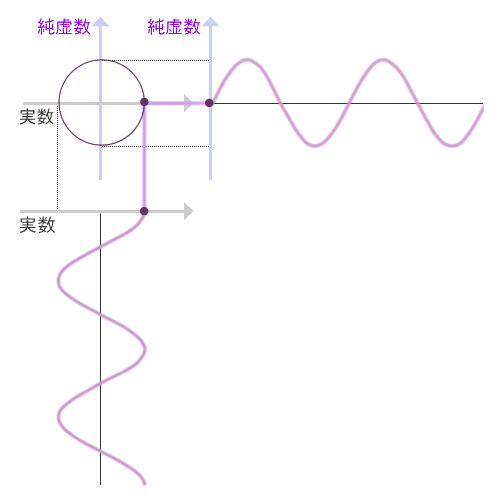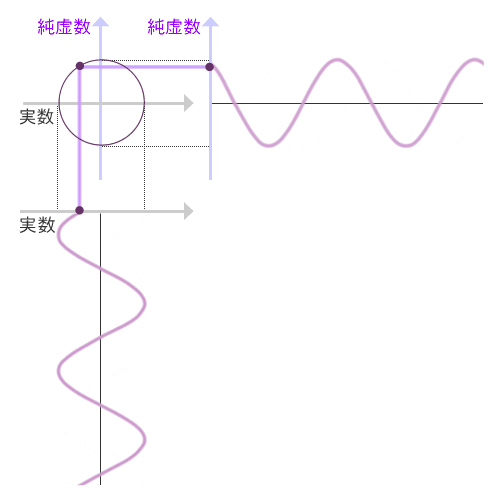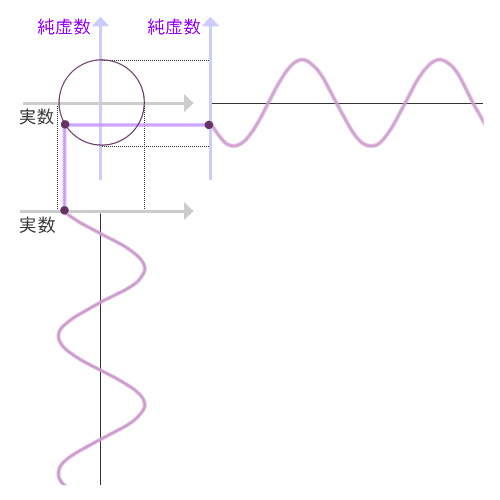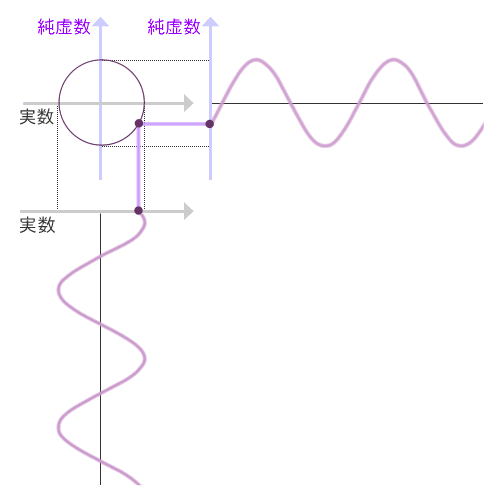
ちょっと脱線します。2回かけてマイナスになる数というのはひとつだけなのでしょうか?
その点について、数を拡張したものがあります。2回かけて -1 になる数として i, j, k というのを導入して、それぞれのあいだでのかけ算の法則を決めてやります。
そうやってできた数のことをハミルトンの四元数といいます。四元数は3次元の回転を表すことができます。四元数はクオータニオンとも呼ばれているのですが、ゲームとかで回転を記述するのにも使ったりするんだそうです。 複素平面や四元数による空間は、実はベクトルの内積の構造が違うので、ミンコフスキー空間にはならなくて、普通のいわゆるユークリッド空間になっています。これらをミンコフスキー空間と関連付けるためには、四元数を拡張したり、もしくは分解型複素数や分解型四元数などを導入する必要があります。
分解型複素数を考えるときは、二乗するとプラス1になる何か(実数じゃないなにか)を導入して、虚数単位 i の代りに使うのです。そうすると、分解型複素数同士のかけ算が、ミンコフスキー空間での内積と同じ演算となるので、こうしてできた分解型複素数の作る平面は2次元ミンコフスキー空間になっています。
興味のある人はWikipediaで調べてみてください。ただし、この記事を書いている時点では分解型四元数についての日本語のページはなくて、英語のページを見ないといけなかったですが。それにこの記事とは違って数式がいっぱいになっています。 さて、早足でしたが、複素数と複素平面について話してみました。
私が学生のころは、高校で複素平面について習ったものですが、今はやらないみたいですね。
もっと詳しく知りたい人は複素数とかで調べてみるといいでしょう。
|