|
普通、動いている物体から投げた物体の速さは両者の速さの和となります。ところが光速度一定の原理によれば、光源が移動していようが止まっていようが光の速度は一定だというのです。
速さというのは移動距離を経過時間で割ったものですが、その速さが一定ということになると、この距離と時間に変形が加わってきます。
時間の縮みから考えるのが楽でしょう。
以下の図を見て下さい。
左が止まっているときの様子です。2枚の鏡のあいだを光が反射しています。鏡の間の距離を光速で割ってやると光が鏡のあいだを往復するのに要する時間がでてきます。では、鏡が移動しているとどうでしょう。鏡といっしょに移動している人にとっては左の図と同じように見えるのですが、移動していない人にとって、光はななめに移動しているのが見えるはずです。そうすると、光の移動した距離はななめの線となりますから、当然鏡の間の距離よりも伸びますね。ところが、移動してる人にとっても止まってる人にとっても光速度は一定ですから、移動してる人にとっての光の往復時間を止まってる人が計算すると、伸びた移動距離を光速度で割るわけですから、経過時間が伸びることになります。つまり、止まってる人から見て、移動してる人の時間はゆっくりと経過することにならないとつじつまがあわなくなることになります。
(実際にどのくらい時間が変化するのか計算してみるとわかるのですが、この考え方で時間の縮みは計算することができます。)
では、距離の方はどうでしょうか。これは時間がゆっくり進むことを利用すればすぐ出ます。以下の図を見て下さい。

動いているロケットの後端から先端にむけて光を発射しています。
止まってるときに光の到達時間と光速度をかけてやれば部屋の長さが求まります。動いてるときに、止まってる人が光を観測すると、光が後端から先端に到達する時間は止まってるときより短くなります。ところが光速度はどちらで見ても同じですから、距離は当然短くなります。これが有名なローレンツ収縮というものです。
ここでするどい人はあれ?と思ったことでしょう。動いてる物体の中で光が進んでいるのに、二つ目の図では距離が縮んでるのに対して、最初の図ではそのままだと。
これは物理ではよく使う方法なのですが、速度の方向とそれ以外を分解してしまうのです。速度の方向は「速度がある」という性質のために他と区別できるのですが、速度の方向と直交してる方向は速度がないので、他と区別することができないのです。(直交する方向に影響するような現象もありますが……)
最初の図では鏡は移動する方向と直交している向きにあるためその距離は影響を受けません。それに対して、二つ目の図ではロケットの進行方向と光の進行方向が一致しているので、距離が影響を受けるのです。
上で用いた考え方は単にピタゴラスの定理と速さの公式(=距離÷時間)を用いただけですから、特殊相対論の計算は高校程度の数学の知識があれば十分理解できることになります。
アインシュタインの先生だったミンコフスキーという人は、この性質についての洞察を深くしていって、問題をさらに抽象化することに成功しました。世によくあるパラドクスを解くにはこの方式を用いた方がいいので、それについても説明しましょう。
このローレンツ収縮をよく考えてみると、時間と空間が同じようにして変化してることがわかります。そこでミンコフスキーは時間と空間をひとつの平面として表すことによって、特殊相対性理論での現象を幾何学的に表現することができることを示したのです。
下の図を見て下さい。
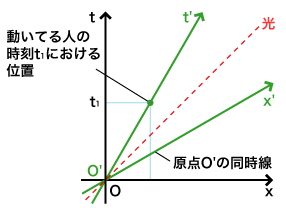
これが止まってる人と動いてる人についての時間と空間をひとつのグラフにまとめたものです。t,t'が時間軸で、x,x'が動いている人の進行方向の長さの軸。ふたりは原点O=O'ですれ違います。動いてる人O'にとって、自分はずっと原点にとまってることになりますから、軸t'は動いてる人にとっての位置0を表します。t'軸のかたむきが動いてる人の移動速度を表します。点線の斜線は光の経路です。これはどの立場から見ても同じになります。つまり、動いてる人にとっても止まってる人にとっても光の速さは同じになるということです。この図の特徴はt'軸だけでなく、x'軸もかたむいてることにあります。x'軸はt'=0の線ですから、動いてる人と止まってる人がすれ違った瞬間と同じ時刻を意味することになります。図は光の経路について対称になってます。
これは動いてる人を主体にして書くこともできます。
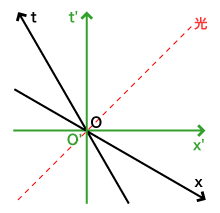
さて、x'軸が動いてる人にとっての同時だと言いましたね。するとx軸は?もちろん、これはt=0の同時線になります。ところが図を見てもらえばすぐわかると思いますが、一方にとっての同時は他方にとっての同時ではないということになるのです。
空間的に離れた点で起きた現象が、移動する速度によって同時かどうかが違ってしまうというのが特殊相対性理論の帰結のひとつなのです。
普通、距離が離れてる点同士の連絡は光によってしかできないので、この同時のずれは破壊的な現象を導くことはありません。しかし、SFでおなじみの超光速通信やワープなどを導入するとかなり致命的な回避不能なパラドクスが生じてしまいます。
それを題材にしたのが「“トリッキー”なパラドックス」です。
“トリッキー”なパラドックスについての相対論的な解釈はこちらに書いてみます。
次回は他のよく言われるパラドクスについて述べましょう。
|